Find the particular solution of the following differential equation.
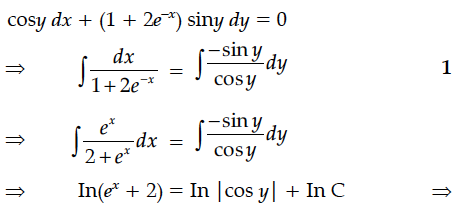
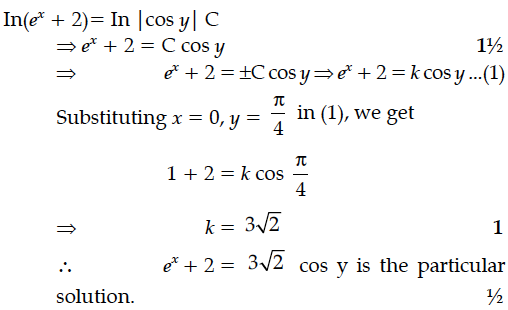
Find the particular solution of the following differential equation :
y = 0 when x = 0.
Find the particular solution of the following differential equation :
y = 0, when x = 2.
Let f : W → W be defined as show that f is invertible. Find the inverse of f,where W is the set of all whole numbers.
Find the general solution of the differential equation (1 + tan y)(dx – dy) + 2xdy = 0.
Let f : N → R be a function defined as f(x) = 4x² + 12x + 15. Then show that f : N → S, where S is range of f, is invertible. Also find the inverse of f.
If the function f : R → R be given by f(x) = x² + 2 and g : R → R be given by g(x) = find fog and gof and hence find fog(2) and gof(– 3).
Solve the differential equation + given that y = 1 when x = 1.
