Write the number of vectors of unit length perpendicular to both the vector →a=∧2i+∧j+∧2k and →b=ˆj+ˆk.
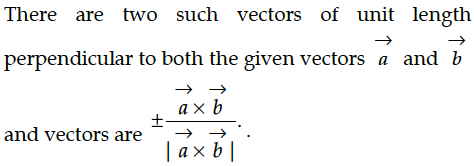
Find the area of the parallelogram whose diagonals are represented by the vectors →a = 2ˆi−3ˆj+4ˆk and →b=2ˆi−ˆj+2ˆk
Write the degree of the differential equation : (d2ydx2)2−2d2ydx2−dydx+1=0.
Find the position vector of a point which divides the join of points with position vectors →(a−2→b) and →(2a+→b) externally in the ratio 2 : 1.
If R = {(x, y) : x + 2y = 8} is a relation on N, writethe range of R.
For what value of λ are the vectors ∧i+2λ∧j+∧k and 2∧i+∧j−3∧k perpendicular ?
If A is a square matrix and | A | = 2, then write the value of | AA’ |, where A’ is the transpose of matrix A.
Using derivative, find the approximate percentage increase in the area of a circle if its radius is increased by 2%.
