Question

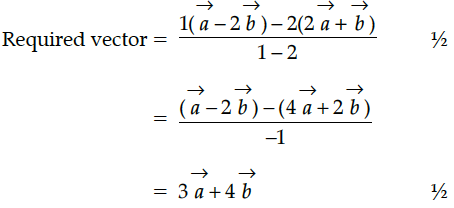
Write the position vector of the point which divides the join of points with position vectors $3\stackrel{\rightarrow}{a}-2\stackrel{\rightarrow}{b}$ and $2\stackrel{\rightarrow}{a}+3\stackrel{\rightarrow}{b}$ in the ratio 2:1.

Find the position vector of a point R, which divides the line joining two points P and Q whose position vectors are $2\stackrel{\rightarrow}{a}+\stackrel{\rightarrow}{b}$ and $\stackrel{\rightarrow}{a}-3\stackrel{\rightarrow}{b}$ respectively, externally in the ratio 1 : 2 Also, show that P is the mid-point, of line segment RQ.

Find $|\stackrel{\rightarrow}{x}|\$, if for a unit vector $\stackrel{\rightarrow}{a}\$ and ($\stackrel{\rightarrow}{x}\$ + $\stackrel{\rightarrow}{a}\$ )($\stackrel{\rightarrow}{x}\$ -$\stackrel{\rightarrow}{a}\$ ) = 15.

Write a unit vector in the direction of vector $\stackrel{\rightarrow}{PQ}\$ where $\stackrel{\rightarrow}{p}\$ and $\stackrel{\rightarrow}{q}\$ are the points (1, 3, 0) and (4, 5, 6),respectively,

if $|\stackrel{\rightarrow}{a}+\stackrel{\rightarrow}{b}|$ =60, $|\stackrel{\rightarrow}{a}-\stackrel{\rightarrow}{b}|$=40 and $\stackrel{\rightarrow}{a}\$=22,then find $\stackrel{\rightarrow}{b}\$.

Write the number of vectors of unit length perpendicular to both the vector $\stackrel{\rightarrow}{a}=\stackrel{\wedge}{2i}+\stackrel{\wedge}{j}+\stackrel{\wedge}{2k}$ and ${\vec{b}}={\hat{j}}+{\hat{k}}\,.$

P and Q are two points with position vectors $3\stackrel{\rightarrow}{a}-2\stackrel{\rightarrow}{b}$ and $\stackrel{\rightarrow}{a}+\stackrel{\rightarrow}{b}$ respectively. Write the position vector of a point R which divides the line segment PQ externally in the ratio 2 : 1.