Question

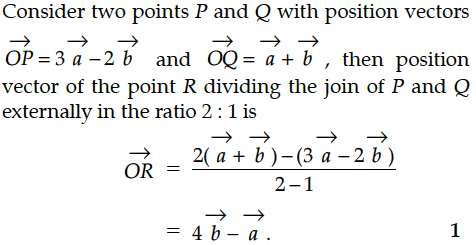
L and M are two points with position vectors $2\stackrel{\rightarrow}{a}-\stackrel{\rightarrow}{b}$ and $\stackrel{\rightarrow}{a}+2\stackrel{\rightarrow}{b}$ respectively. Write the position vectors of a point N which divides the line segment LM in the ratio 2:1 externally.

Find the position vector of a point which divides the join of points with position vectors $\;\stackrel{\rightarrow}{(a}-2\stackrel{\rightarrow}{b})$ and $\;\stackrel{\rightarrow}{(2a}+\stackrel{\rightarrow}{b})$ externally in the ratio 2 : 1.

if $|\stackrel{\rightarrow}{a}+\stackrel{\rightarrow}{b}|$ =60, $|\stackrel{\rightarrow}{a}-\stackrel{\rightarrow}{b}|$=40 and $\stackrel{\rightarrow}{a}\$=22,then find $\stackrel{\rightarrow}{b}\$.

Write the position vector of the point which divides the join of points with position vectors $3\stackrel{\rightarrow}{a}-2\stackrel{\rightarrow}{b}$ and $2\stackrel{\rightarrow}{a}+3\stackrel{\rightarrow}{b}$ in the ratio 2:1.

If $|\stackrel{\rightarrow}{a}|$=2, $|\stackrel{\rightarrow}{b}|$=3 and $\stackrel{\rightarrow}{a}$.$\stackrel{\rightarrow}{b}$=3 then find the projection of $|\stackrel{\rightarrow}{b}|$ on $|\stackrel{\rightarrow}{a}|$.

Find the position vector of a point R, which divides the line joining two points P and Q whose position vectors are $2\stackrel{\rightarrow}{a}+\stackrel{\rightarrow}{b}$ and $\stackrel{\rightarrow}{a}-3\stackrel{\rightarrow}{b}$ respectively, externally in the ratio 1 : 2 Also, show that P is the mid-point, of line segment RQ.

Write a unit vector in the direction of vector $\stackrel{\rightarrow}{PQ}\$ where $\stackrel{\rightarrow}{p}\$ and $\stackrel{\rightarrow}{q}\$ are the points (1, 3, 0) and (4, 5, 6),respectively,