Write a vector in the direction of the vector that has magnitude 9 units.

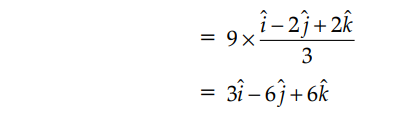
Find the scalar components of the vector with initial point A(2,1) and terminal point B (– 5, 7).
Let f : R → R be defined by f(x) = 3x² – 5 and g : R → R be defined by g(x) = find gof(x) .
What is the degree of the following differential equation ?
If is the cofactor of the element of the determinant , then write the value of
